Teaching My Machine to Play Tic-Tac-Toe
I spent the last few mornings writing a program that plays an optimal game of Tic-Tac-Toe:
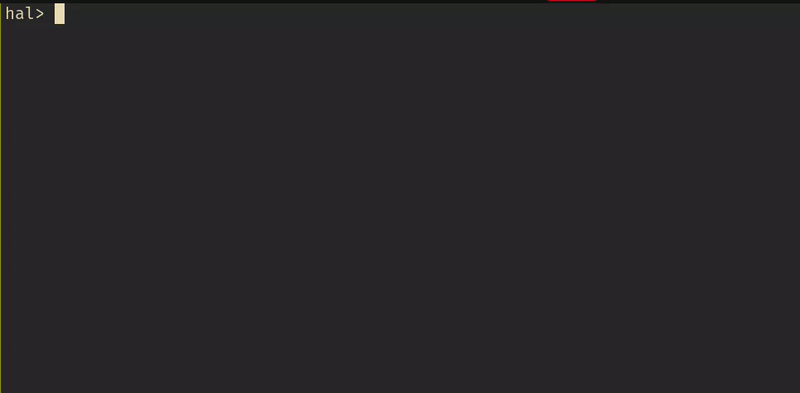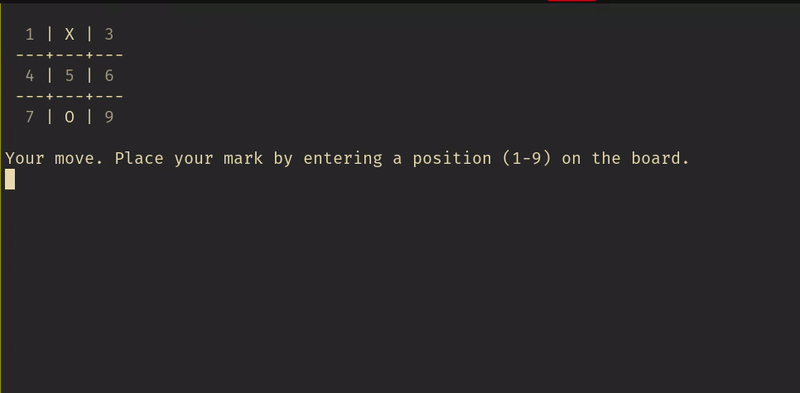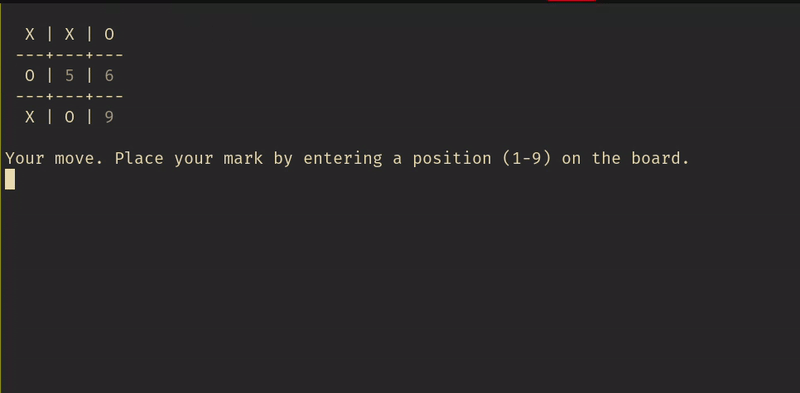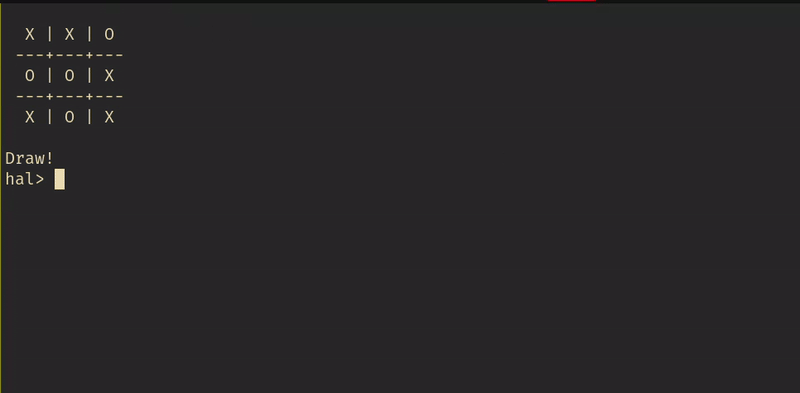
I anticipated it would take me an hour to get something working, and another hour or two to polish it. As usual, I was off by a factor of 2 or 3 here.
What ended up being trickier than I anticipated was how to calculate an optimal move for the machine. I’m still not positive I’ve got it correct. Here’s the relevant bit of code that performs this calculation:
fn optimal_move_and_outcome(&self, mark: Mark) -> (Board, Outcome) {
match self.check_outcome() {
Some(outcome) => (self.clone(), outcome),
None => {
let mut futures = self
.moves_for(mark)
.map(|board| {
let (_, o) = board.optimal_move_and_outcome(mark.opposite());
(board, o)
})
.collect::<Vec<(Board, Outcome)>>();
futures.sort_by(|(_, o1), (_, o2)| mark.better(*o1, *o2));
futures.pop().expect("failed to consider any moves")
}
}
}
optimal_move_and_outcome is a recursive function traverses the game tree
depth-first.
For each possible future tic-tac-toe board, it asks:
- Does this board constitute a completed game? If so, the result is the board and the outcome (either a win for X, a win for O, or a draw).
- If the game isn’t over, consider all possible moves that the other player could make (along with their outcomes). Order them according to what’s better for the other player, and pick the best one from their point of view.
So optimal_move_and_outcome calculates a next move along with an outcome.
These satisfy the following guarantee: if both players make optimal moves
hereafter, then making the move described by the board I returned will result in
the outcome I returned.
This is all assuming the (human) opponent plays optimally, though.
What I’m still trying to figure out is this: is it possible for the other player
to make a suboptimal move in the future in such a way that the outcome
returned by optimal_move_and_outcome is no longer guaranteed?
And I’m almost positive this isn’t the case.
That is, there’s a kind of “monotonic” quality to optimal_move_and_outcome
that says, “if you make the move represented by this board, you’re guaranteed an
outcome at least as good as the one I returned; if your opponent plays
suboptimally at some point, you could do even better, but you’ll never do
worse.”
That’s because optimal_move_and_outcome is considering every possible future
sequence of moves: so the notion of a “locally suboptimal but globally optimal”
move isn’t quite coherent.
This feels like the kind of result that shouldn’t be too difficult to prove by induction. At some point I should try formalizing it in Lean.
Final Thoughts
Despite playing around with Rust on and off for the last several years, this was
my first “real” Rust program.
And the language really shined.
The availability of basic traits like Display and Default resulted in really
simple code for rendering and initializing the components of the game; sum types
(via enum) were the right fit for representing marks and game outcomes; the
fact that I/O functions return Results instead of setting an out-of-band error
code greatly simplified the terminal interactions; the ease with which I could
define a custom Ordering on a type, and use it to sort a Vec of its
inhabitants made the minimax calculation straightforward; and much more besides.
But I’m probably most proud of my decision to iterate over all possible
3-in-a-row “lines” using a custom Iterator:
struct LineIter<'a> {
board: &'a Board,
idx: usize,
}
// A representation of a line of grid spaces on a board.
struct Line([Option<Mark>; 3]);
impl<'a> Iterator for LineIter<'a> {
type Item = Line;
fn next(&mut self) -> Option<Line> {
let line = match self.idx {
0 => Some([0, 1, 2]),
1 => Some([3, 4, 5]),
2 => Some([6, 7, 8]),
3 => Some([0, 3, 6]),
4 => Some([1, 4, 7]),
5 => Some([2, 5, 8]),
6 => Some([0, 4, 8]),
7 => Some([2, 4, 6]),
_ => None,
};
if self.idx < 8 {
self.idx += 1
}
line.map(|coords| Line(coords.map(|i| self.board.0[i])))
}
}
This is used when checking if a board represents a completed game, a calculation
that requires looking at every row, every column, and the two diagonals on a
board.
With LineIter, we can just write something like this:
/// Check if this board contains a winning "line" or marks, or represents a
/// draw (in the event that no more marks can be placed).
pub fn check_outcome(&self) -> Option<Outcome> {
for line in self.lines() {
let x_line = line.0.iter().all(|cell| *cell == Some(Mark::X));
if x_line {
return Some(Outcome::Win(Mark::X));
}
let o_line = line.0.iter().all(|cell| *cell == Some(Mark::O));
if o_line {
return Some(Outcome::Win(Mark::O));
}
}
let all_filled = self.0.iter().all(Option::is_some);
if all_filled {
return Some(Outcome::Draw);
}
None
}
fn lines(&self) -> LineIter {
LineIter {
board: self,
idx: 0,
}
}